
Open the Right Doors to Win a Car
Open the Right Doors to Win a Car
Two people are allowed to open 2 out of 3 doors. If behind those doors are the car and the car key, they win the car.
Alex Bellos presented this riddle on The Guardian as follows:

Twin brothers Timmy and Tammy are contestants on a game show. They will take turns opening 2 out of 3 doors. Behind the doors are a car, a car key, and a goat, placed randomly. They don't know which item is behind which door.
Timmy goes on stage first. He opens 2 of the 3 doors, then closes them again and exits to a separate room. Then Tammy comes on stage and also opens 2 of the 3 doors.
If Timmy opens the door with the car and Tammy opens the door with the key, the twins win the car. In all other cases, they win nothing.
The twins are given 10 minutes beforehand to plan a strategy to maximize their chances of winning.
What should their strategy be, and what is the highest probability they can achieve?
Solution:
There are 3 doors, and behind them randomly are:
-
A car (C)
-
A key (K)
-
A goat (G)
Let’s label the doors: A, B, and C.
Timmy goes first. He opens any 2 doors, sees what’s behind them, closes them, and leaves. Then Tammy opens 2 doors. They win only if Timmy opens the door with the car and Tammy opens the door with the key.
Here's the challenge: Tammy doesn’t know what Timmy saw, and they can't communicate. So their only chance is to agree on a strategy beforehand that allows Tammy to deduce where the key is based on which doors she opens and what she finds.
Let’s think carefully. The total number of ways to randomly assign C, K, G behind 3 doors is 6 (3! permutations):
-
C-K-G
-
C-G-K
-
K-C-G
-
K-G-C
-
G-C-K
-
G-K-C
Each placement is equally likely.
Key Insight:
Timmy sees the contents behind 2 doors. That means he knows 2 out of the 3 items (but not necessarily their exact identities, unless he sees both the car and the key).
Timmy’s role is to encode information by which 2 doors he chooses to open. That way, Tammy, by following the agreed strategy, can infer where the key is, depending on what she finds.
Let’s define a strategy:
-
The twins agree to map each of the 6 permutations to a specific pair of doors Timmy will open.
-
When Timmy sees a configuration (e.g., he sees the car and goat), he uses a code to select 2 doors that encode where the key is.
-
Tammy then uses the agreed strategy to decode Timmy’s message and pick the right door for the key.
It turns out this is possible.
What’s the maximum probability?
Because there are 6 possible assignments of C, K, and G to 3 doors, and Timmy can choose 3 possible pairs of doors to open (3 choose 2 = 3 combinations: AB, AC, BC), but each pair could be ordered or interpreted in different ways (e.g., based on order of opening, or what is revealed), it is possible to construct a coding strategy that covers all 6 cases uniquely.
So:
✅ With a well-designed strategy, they can always win.
🎯 The maximum probability of success is 100%.
Conclusion:
The twins can win the car 100% of the time if they use a clever encoding-decoding strategy agreed upon before the game. Timmy uses the two doors he opens to encode the location of the key, and Tammy uses their strategy to decode and find it.
News in the same category


What Is the Spiritual Significance of a Black Cat?

Who Will Accidentally Get Hurt First?
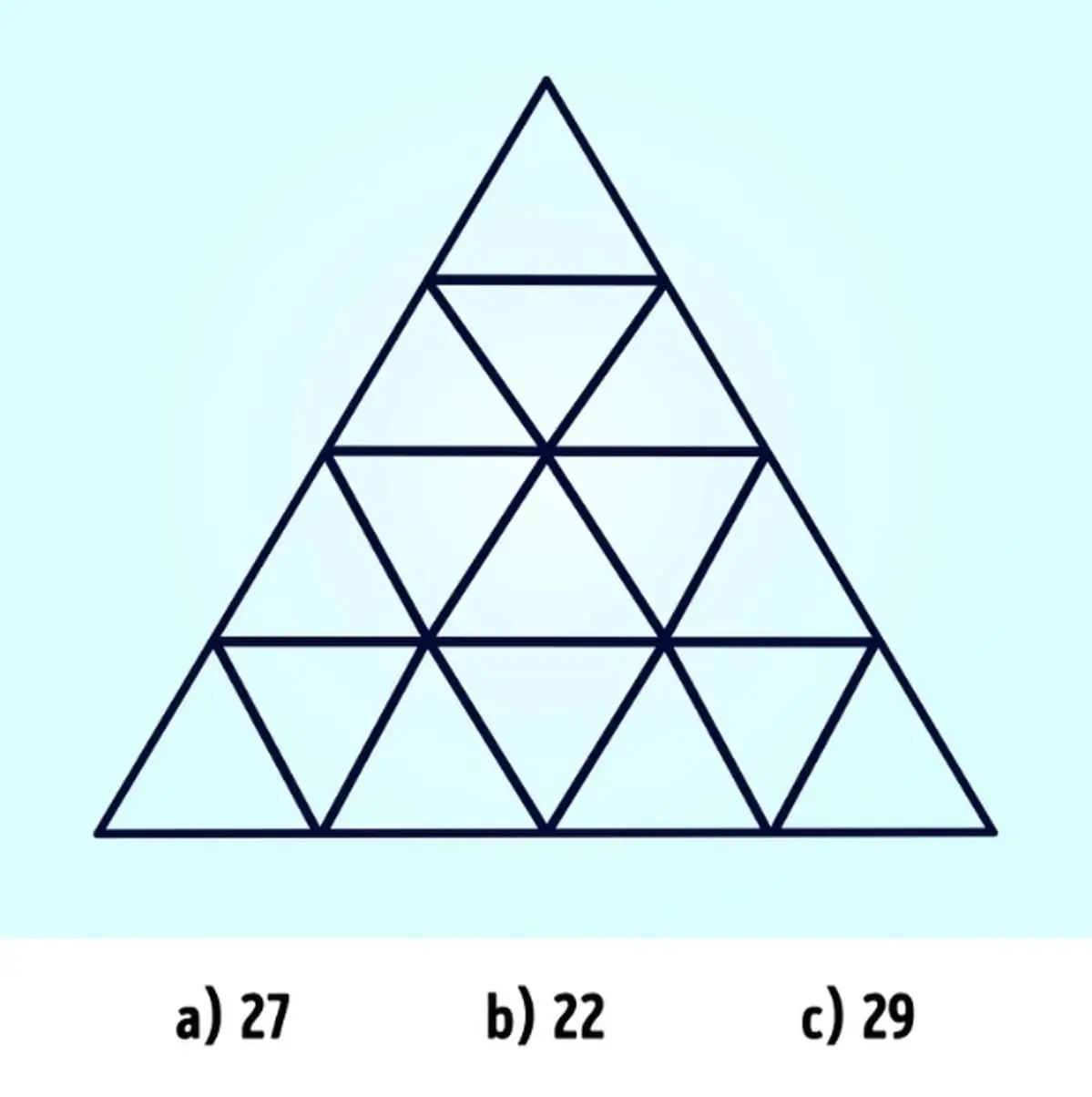
Only Those with High IQ Can Count the Exact Number of Triangles in This Image
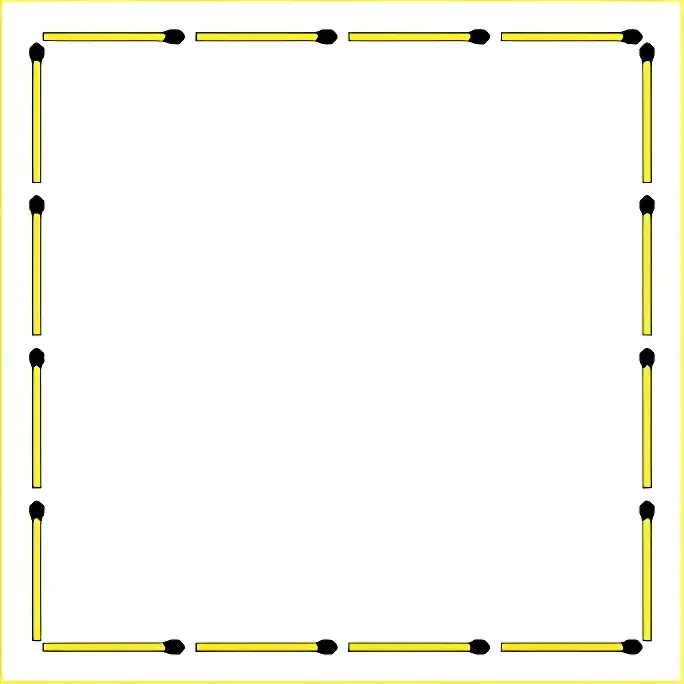
Add 9 matchsticks to divide the shape into 4 equal parts

Why Do Many Believe the Poor Avoid Buying Second-Floor Homes, While the Wealthy Skip the 18th Floor?

Only 2% With Most Attentive Eyes Can Spot the Mistake in 4 Seconds!

6 tips from billionaires to help you 'make money'
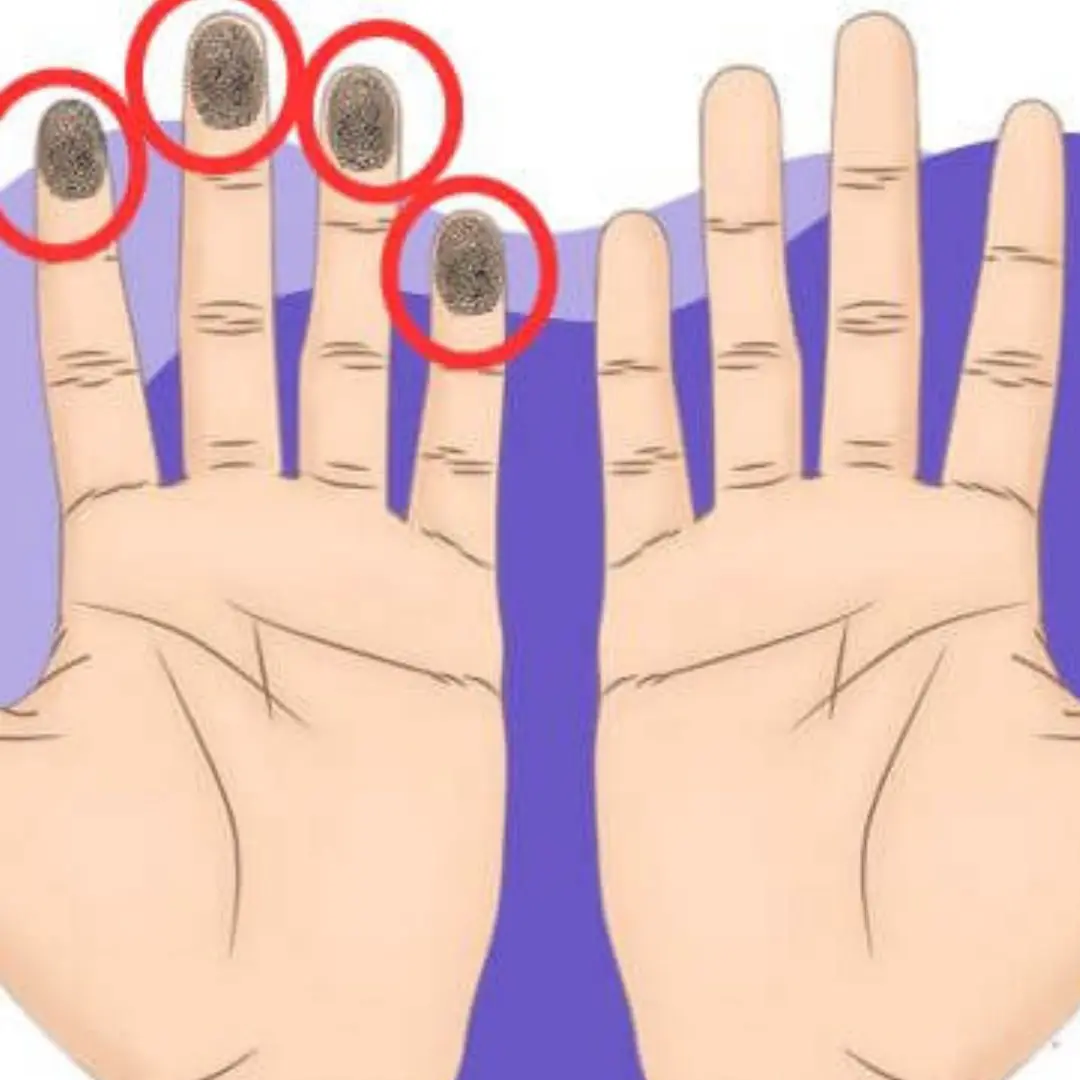
How many fingertip whorls do you have? The number of whorls you have could reveal secrets about your future
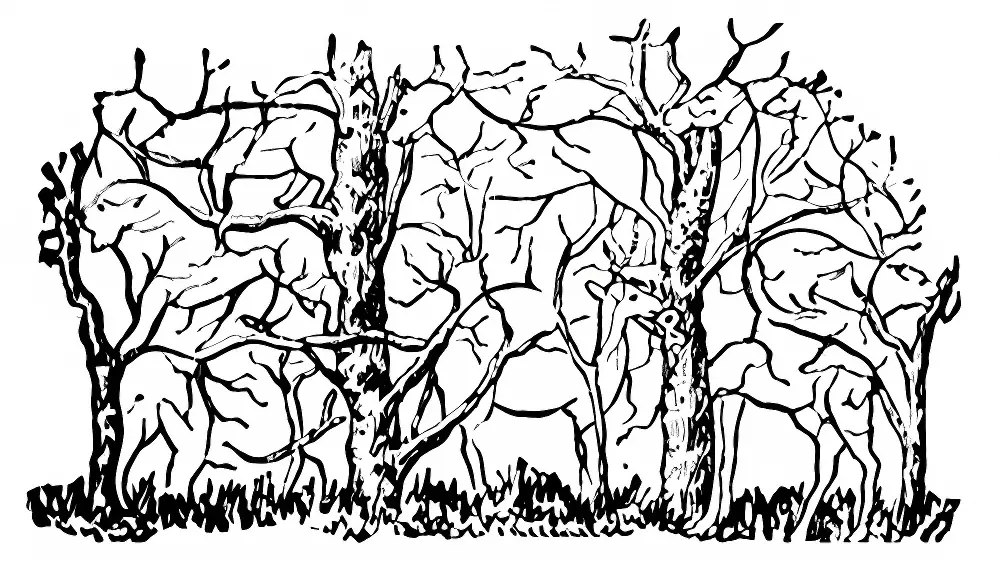
Can You Spot How Many Animals Are in the Tree?

Can you see all four ducks, or do you need 20/20 vision like me?

What Should the Young Man Do to Escape Danger?

Who is the mother of the boy playing in the picture below?

Doctors advise tired women to look at muscular men often

Quiz you find the hidden face in the picture in 3 seconds

The little hole near your sink’s rim? It’s more useful than you think

For those of you who don't understand
The Shape of Your Ears Can Reveal Your Personality and Fortune

Where Is the Snake Hiding?

The First Animal You See Reveals Something Amazing About Your Personality
News Post

The Most Nutritious Part of the Chicken—“Pricier than Gold” Yet Often Thrown Away by Home Cooks
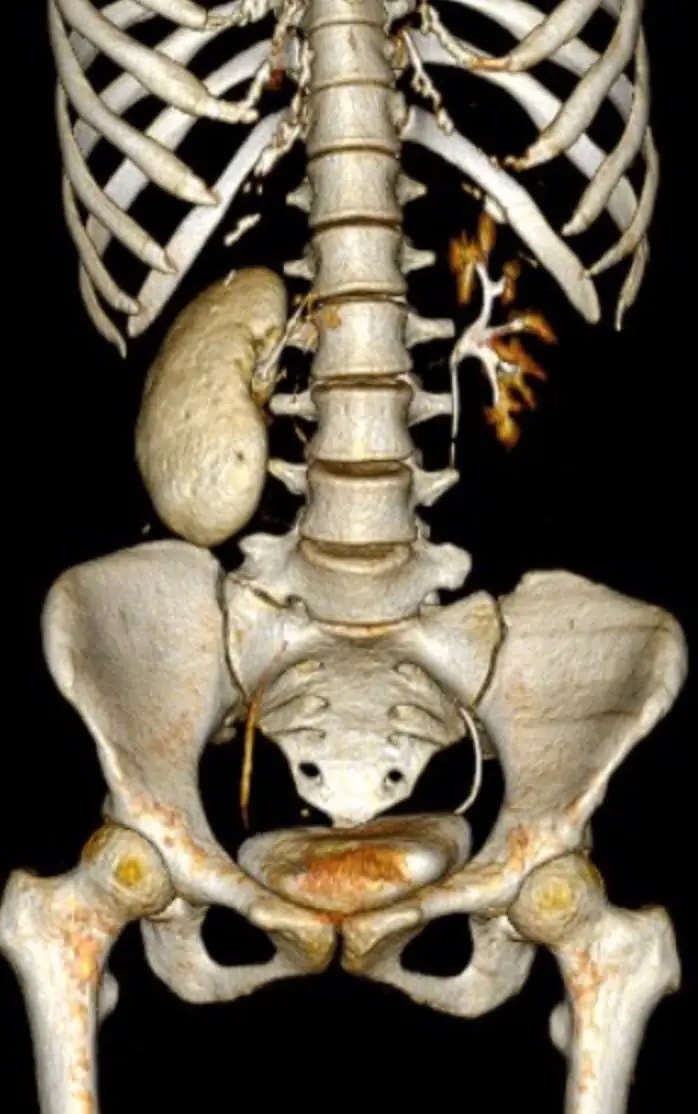
Doctor Urges 4 Actions to Protect Your Body’s "Blo.od Filter"

6 Smart Tips for Choosing Quality Honey Sellers Don’t Want You to Know

Can overly hot baths harm your heart and circulation?
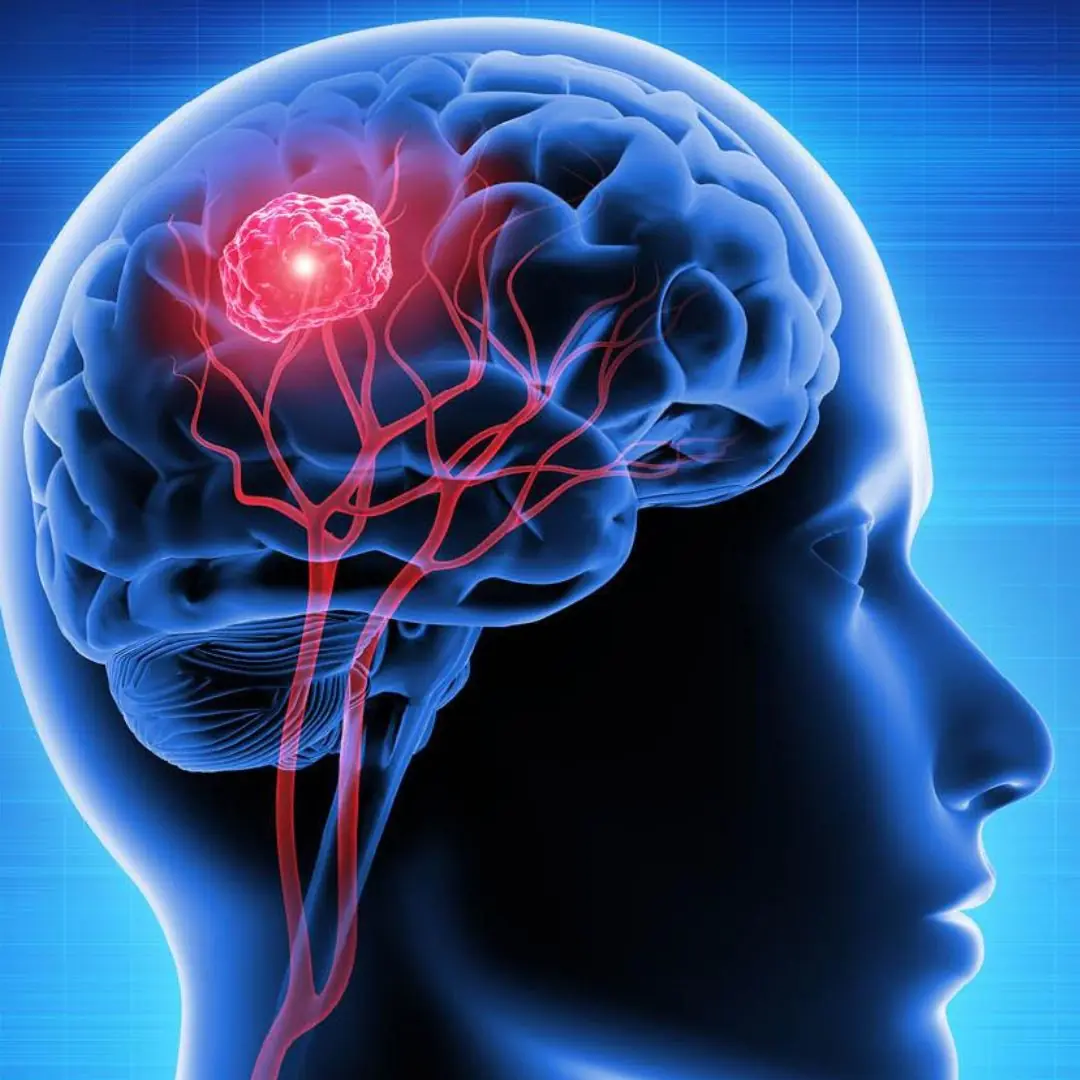
7 signs of brain c.a.ncer that are easily confused with other diseases

4 Things to Avoid After 5 PM to Lower Your Risk of Stro.ke

Doctors Warn: This Common Way of Eating Boiled Eggs Can Clog Your Arteries

Blanch Bones First or Simmer Directly?

2 Common Vegetables That Can Harbor Parasites

The 'Vitamin C King' of the Vegetable World

Avoid Swimming If You Spot 'Square Waves'

3 Green Vegetables Called the “King” of Sto.mach Protection

Why You Should Not Bring Seeds on a Plane: A Detailed Explanation
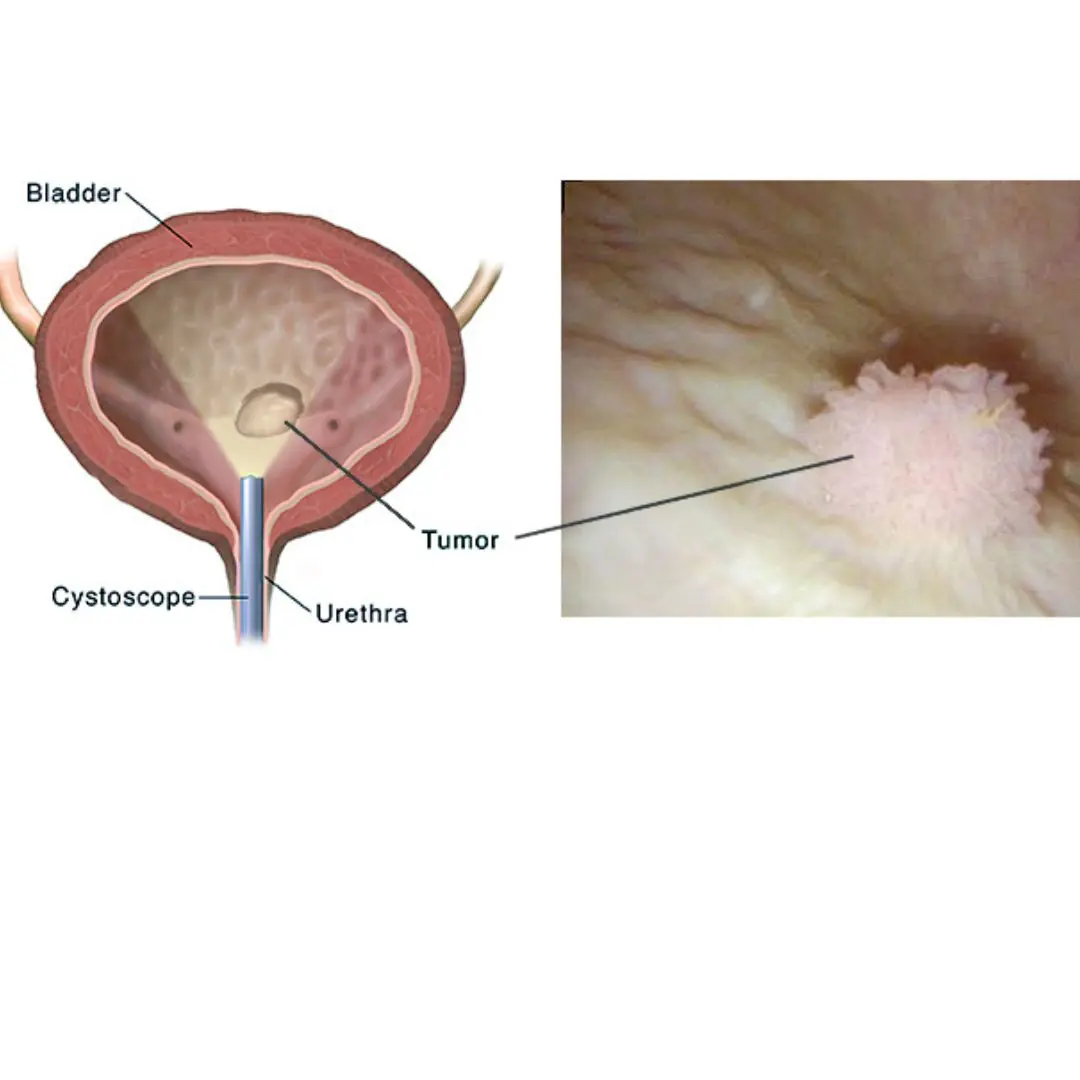
Bladder Ca.ncer: Symptoms You Shouldn’t Ignore
4 Healing Drinks to Prevent and Dissolve Kidney Stones

10 Powerful Reasons a Simple Smile Can Change Your Life

The Surprising Benefits of Donating Bl.o.od

5 types of vegetables and fruits help cool the liver and effectively lower liver enzymes

Top vegetable to help reduce visceral fat extremely effectively, nutritionist reveals 4 more easy ways to lose weight
